Portal:Mathematics

---

The Mathematics Portal

Euclid

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Featured articles –

  Featured articles are displayed here, which represent some of the best content on English Wikipedia.

---

• 

  

  The weighing pans of this balance scale contain zero objects, divided into two equal groups.

  
  In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
  
  Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
• 
  
  

  

  Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

  
  An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.
  
  While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in 17th-century studies of probability and annuities. Actuaries in the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems; actuaries use this knowledge to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...)
• 

  

  Logic studies valid forms of inference like modus ponens.

  
  
  Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.
  
  Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work." Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
• 

  

  High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

  
  
  General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.
  
  By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
• 

  

  
  Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.
  
  Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...)
• 
  General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever is
  present, including matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.
  
  Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)
• 
  
  

  

  Noether c. 1900–1910

  
  Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She also proved Noether's first and second theorems, which are fundamental in mathematical physics. Noether was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.
  
  Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
• 
  
  

  

  Rejewski, c. 1932

  
  Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ^ⓘ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.
  
  Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
• 
  In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.
  
  Thus hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)
• 
  
  

  

  One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)

  
  Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.
  
  Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...)
• 
  
  

  

  Portrait by Jakob Emanuel Handmann, 1753

  
  Leonhard Euler (/ˈɔɪlər/ ^ⓘ OY-lər; Swiss Standard German: [ˈleːɔnhard ˈɔʏlər]; German: [ˈleːɔnhaʁt ˈɔʏlɐ] ^ⓘ; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.
  
  Euler is credited for popularizing the Greek letter $\pi$ (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation $f(x)$ for the value of a function, the letter $i$ to express the imaginary unit ${\sqrt {-1}}$, the Greek letter $\Sigma$ (capital sigma) to express summations, the Greek letter $\Delta$ (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant $e$, the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)
• 

  

  Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).

  
  
  In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
  It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
  and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.
  
  The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)
• 

  

  Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

  
  
  In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).
  
  In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)
• 
  
  

  

  Elementary algebra studies which values solve equations formed using arithmetical operations.

  
  Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.
  
  Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
• 
  
  

  

  The title page of a 1634 version of Hues' Tractatus de globis in the collection of the Biblioteca Nacional de Portugal

  
  Robert Hues (1553 – 24 May 1632) was an English mathematician and geographer. He attended St. Mary Hall at Oxford, and graduated in 1578. Hues became interested in geography and mathematics, and studied navigation at a school set up by Walter Raleigh. During a trip to Newfoundland, he made observations which caused him to doubt the accepted published values for variations of the compass. Between 1586 and 1588, Hues travelled with Thomas Cavendish on a circumnavigation of the globe, performing astronomical observations and taking the latitudes of places they visited. Beginning in August 1591, Hues and Cavendish again set out on another circumnavigation of the globe. During the voyage, Hues made astronomical observations in the South Atlantic, and continued his observations of the variation of the compass at various latitudes and at the Equator. Cavendish died on the journey in 1592, and Hues returned to England the following year.
  
  In 1594, Hues published his discoveries in the Latin work Tractatus de globis et eorum usu (Treatise on Globes and Their Use) which was written to explain the use of the terrestrial and celestial globes that had been made and published by Emery Molyneux in late 1592 or early 1593, and to encourage English sailors to use practical astronomical navigation. Hues' work subsequently went into at least 12 other printings in Dutch, English, French and Latin. (Full article...)

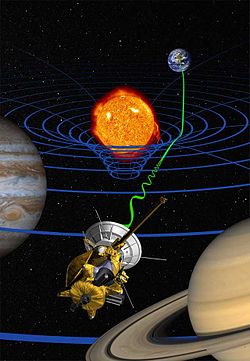
Selected image –

spiral figure representing both finite and transfinite ordinal numbers

Ordinal numbers

Credit: Pop-up casket & Fool

This spiral diagram represents all ordinal numbers less than ω^ω. The first (outermost) turn of the spiral represents the finite ordinal numbers, which are the regular counting numbers starting with zero. As the spiral completes its first turn (at the top of the diagram), the ordinal numbers approach infinity, or more precisely ω, the first transfinite ordinal number (identified with the set of all counting numbers, a "countably infinite" set, the cardinality of which corresponds to the first transfinite cardinal number, called ℵ₀). The ordinal numbers continue from this point in the second turn of the spiral with ω + 1, ω + 2, and so forth. (A special ordinal arithmetic is defined to give meaning to these expressions, since the + symbol here does not represent the addition of two real numbers.) Halfway through the second turn of the spiral (at the bottom) the numbers approach ω + ω, or ω · 2. The ordinal numbers continue with ω · 2 + 1 through ω · 2 + ω = ω · 3 (three-quarters of the way through the second turn, or at the "9 o'clock" position), then through ω · 4, and so forth, up to ω · ω = ω² at the top. (As with addition, the multiplication and exponentiation operations have definitions that work with transfinite numbers.) The ordinals continue in the third turn of the spiral with ω² + 1 through ω² + ω, then through ω² + ω² = ω² · 2, up to ω² · ω = ω³ at the top of the third turn. Continuing in this way, the ordinals increase by one power of ω for each turn of the spiral, approaching ω^ω in the middle of the diagram, as the spiral makes a countably infinite number of turns. This process can actually continue (not shown in this diagram) through $\omega ^{\omega ^{\omega }}$ and $\omega ^{\omega ^{\omega ^{\omega }}}$, and so on, approaching the first epsilon number, ε₀. Each of these ordinals is still countable, and therefore equal in cardinality to ω. After uncountably many of these transfinite ordinals, the first uncountable ordinal is reached, corresponding to only the second infinite cardinal, $\aleph _{1}$. The identification of this larger cardinality with the cardinality of the set of real numbers can neither be proved nor disproved within the standard version of axiomatic set theory called Zermelo–Fraenkel set theory, whether or not one also assumes the axiom of choice.

Good articles –

  These are Good articles, which meet a core set of high editorial standards.

---

• 
  Vedic Mathematics is a book written by Indian Shankaracharya Bharati Krishna Tirtha and first published in 1965. It contains a list of mathematical techniques which were falsely claimed to contain advanced mathematical knowledge. The book was posthumously published under its deceptive title by editor V. S. Agrawala, who noted in the foreword that the claim of Vedic origin, made by the original author and implied by the title, was unsupported.
  
  Neither Krishna Tirtha nor Agrawala were able to produce sources, and scholars unanimously note it to be a compendium of methods for increasing the speed of elementary mathematical calculations sharing no overlap with historical mathematical developments during the Vedic period. Nonetheless, there has been a proliferation of publications in this area and multiple attempts to integrate the subject into mainstream education at the state level by right-wing Hindu nationalist governments. (Full article...)
• 

  

  The Shapley–Folkman lemma is illustrated by the Minkowski addition of four sets. The point (+) in the convex hull of the Minkowski sum of the four non-convex sets (right) is the sum of four points (+) from the (left-hand) sets—two points in two non-convex sets plus two points in the convex hulls of two sets. The convex hulls are shaded pink. The original sets each have exactly two points (shown as red dots).

  
  The Shapley–Folkman lemma is a result in convex geometry that describes the Minkowski addition of sets in a vector space. It is named after mathematicians Lloyd Shapley and Jon Folkman, but was first published by the economist Ross M. Starr.
  
  The lemma may be intuitively understood as saying that, if the number of summed sets exceeds the dimension of the vector space, then their Minkowski sum is approximately convex. (Full article...)
• 
  
  

  

  Maxwell, c. 1870s

  
  James Clerk Maxwell FRS FRSE (13 June 1831 – 5 November 1879) was a Scottish physicist and mathematician who was responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism and light as different manifestations of the same phenomenon. Maxwell's equations for electromagnetism achieved the second great unification in physics, where the first one had been realised by Isaac Newton. Maxwell was also key in the creation of statistical mechanics.
  
  With the publication of "A Dynamical Theory of the Electromagnetic Field" in 1865, Maxwell demonstrated that electric and magnetic fields travel through space as waves moving at the speed of light. He proposed that light is an undulation in the same medium that is the cause of electric and magnetic phenomena. The unification of light and electrical phenomena led to his prediction of the existence of radio waves, and the paper contained his final version of his equations, which he had been working on since 1856. As a result of his equations, and other contributions such as introducing an effective method to deal with network problems and linear conductors, he is regarded as a founder of the modern field of electrical engineering. In 1871, Maxwell became the first Cavendish Professor of Physics, serving until his death in 1879. (Full article...)
• 

  

  A well-covered graph, the intersection graph of the nine diagonals of a hexagon. The three red vertices form one of its 14 equal-sized maximal independent sets, and the six blue vertices form the complementary minimal vertex cover.

  
  In graph theory, a well-covered graph is an undirected graph in which the minimal vertex covers all have the same size. Here, a vertex cover is a set of vertices that touches all edges, and it is minimal if removing any vertex from it would leave some edge uncovered. Equivalently, well-covered graphs are the graphs in which all maximal independent sets have equal size. Well-covered graphs were defined and first studied by Michael D. Plummer in 1970.
  
  The well-covered graphs include all complete graphs, balanced complete bipartite graphs, and the rook's graphs whose vertices represent squares of a chessboard and edges represent moves of a chess rook. Known characterizations of the well-covered cubic graphs, well-covered claw-free graphs, and well-covered graphs of high girth allow these graphs to be recognized in polynomial time, but testing whether other kinds of graph are well-covered is a coNP-complete problem. (Full article...)
• 

  

  The cover page of Ars Conjectandi

  
  
  Ars Conjectandi (Latin for "The Art of Conjecturing") is a book on combinatorics and mathematical probability written by Jacob Bernoulli and published in 1713, eight years after his death, by his nephew, Niklaus Bernoulli. The seminal work consolidated, apart from many combinatorial topics, many central ideas in probability theory, such as the very first version of the law of large numbers: indeed, it is widely regarded as the founding work of that subject. It also addressed problems that today are classified in the twelvefold way and added to the subjects; consequently, it has been dubbed an important historical landmark in not only probability but all combinatorics by a plethora of mathematical historians. The importance of this early work had a large impact on both contemporary and later mathematicians; for example, Abraham de Moivre.
  
  Bernoulli wrote the text between 1684 and 1689, including the work of mathematicians such as Christiaan Huygens, Gerolamo Cardano, Pierre de Fermat, and Blaise Pascal. He incorporated fundamental combinatorial topics such as his theory of permutations and combinations (the aforementioned problems from the twelvefold way) as well as those more distantly connected to the burgeoning subject: the derivation and properties of the eponymous Bernoulli numbers, for instance. Core topics from probability, such as expected value, were also a significant portion of this important work. (Full article...)
• 

  

  The convex hull of the red set is the blue and red convex set.

  
  In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.
  
  Convex hulls of open sets are open, and convex hulls of compact sets are compact. Every compact convex set is the convex hull of its extreme points. The convex hull operator is an example of a closure operator, and every antimatroid can be represented by applying this closure operator to finite sets of points.
  The algorithmic problems of finding the convex hull of a finite set of points in the plane or other low-dimensional Euclidean spaces, and its dual problem of intersecting half-spaces, are fundamental problems of computational geometry. They can be solved in time $O(n\log n)$ for two or three dimensional point sets, and in time matching the worst-case output complexity given by the upper bound theorem in higher dimensions. (Full article...)
• 

  

  The square root of 2 is equal to the length of the hypotenuse of a right triangle with legs of length 1 and is therefore a constructible number

  
  
  In geometry and algebra, a real number $r$ is constructible if and only if, given a line segment of unit length, a line segment of length $|r|$ can be constructed with compass and straightedge in a finite number of steps. Equivalently, $r$ is constructible if and only if there is a closed-form expression for $r$ using only integers and the operations for addition, subtraction, multiplication, division, and square roots.
  
  The geometric definition of constructible numbers motivates a corresponding definition of constructible points, which can again be described either geometrically or algebraically. A point is constructible if it can be produced as one of the points of a compass and straightedge construction (an endpoint of a line segment or crossing point of two lines or circles), starting from a given unit length segment. Alternatively and equivalently, taking the two endpoints of the given segment to be the points (0, 0) and (1, 0) of a Cartesian coordinate system, a point is constructible if and only if its Cartesian coordinates are both constructible numbers. Constructible numbers and points have also been called ruler and compass numbers and ruler and compass points, to distinguish them from numbers and points that may be constructed using other processes. (Full article...)
• 

  

  The mutilated chessboard

  
  The mutilated chessboard problem is a tiling puzzle posed by Max Black in 1946 that asks:
  
  

  Suppose a standard 8×8 chessboard (or checkerboard) has two diagonally opposite corners removed, leaving 62 squares. Is it possible to place 31 dominoes of size 2×1 so as to cover all of these squares?

  (Full article...)
• 

  

  A unit cube with a hole cut through it, large enough to allow Prince Rupert's cube to pass

  
  In geometry, Prince Rupert's cube is the largest cube that can pass through a hole cut through a unit cube without splitting it into separate pieces. Its side length is approximately 1.06, 6% larger than the side length 1 of the unit cube through which it passes. The problem of finding the largest square that lies entirely within a unit cube is closely related, and has the same solution.
  
  Prince Rupert's cube is named after Prince Rupert of the Rhine, who asked whether a cube could be passed through a hole made in another cube of the same size without splitting the cube into two pieces. A positive answer was given by John Wallis. Approximately 100 years later, Pieter Nieuwland found the largest possible cube that can pass through a hole in a unit cube. (Full article...)
• 

  

  Fig. 1: A binary search tree of size 9 and depth 3, with 8 at the root.

  
  
  In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The time complexity of operations on the binary search tree is linear with respect to the height of the tree.
  
  Binary search trees allow binary search for fast lookup, addition, and removal of data items. Since the nodes in a BST are laid out so that each comparison skips about half of the remaining tree, the lookup performance is proportional to that of binary logarithm. BSTs were devised in the 1960s for the problem of efficient storage of labeled data and are attributed to Conway Berners-Lee and David Wheeler. (Full article...)
• 
  In number theory, a Wieferich prime is a prime number p such that p² divides 2^p − 1 − 1, therefore connecting these primes with Fermat's little theorem, which states that every odd prime p divides 2^p − 1 − 1. Wieferich primes were first described by Arthur Wieferich in 1909 in works pertaining to Fermat's Last Theorem, at which time both of Fermat's theorems were already well known to mathematicians.
  
  Since then, connections between Wieferich primes and various other topics in mathematics have been discovered, including other types of numbers and primes, such as Mersenne and Fermat numbers, specific types of pseudoprimes and some types of numbers generalized from the original definition of a Wieferich prime. Over time, those connections discovered have extended to cover more properties of certain prime numbers as well as more general subjects such as number fields and the abc conjecture. (Full article...)
• 
  
  

  

  Huygens by Caspar Netscher (1671), Museum Boerhaave, Leiden

  
  Christiaan Huygens, Lord of Zeelhem, FRS (/ˈhaɪɡənz/ HY-gənz, US also /ˈhɔɪɡənz/ HOY-gənz; Dutch: [ˈkrɪstijaːn ˈɦœyɣə(n)s] ^ⓘ; also spelled Huyghens; Latin: Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution. In physics, Huygens made seminal contributions to optics and mechanics, while as an astronomer he studied the rings of Saturn and discovered its largest moon, Titan. As an engineer and inventor, he improved the design of telescopes and invented the pendulum clock, the most accurate timekeeper for almost 300 years. A talented mathematician and physicist, his works contain the first idealization of a physical problem by a set of mathematical parameters, and the first mathematical and mechanistic explanation of an unobservable physical phenomenon.
  
  Huygens first identified the correct laws of elastic collision in his work De Motu Corporum ex Percussione, completed in 1656 but published posthumously in 1703. In 1659, Huygens derived geometrically the formula in classical mechanics for the centrifugal force in his work De vi Centrifuga, a decade before Isaac Newton. In optics, he is best known for his wave theory of light, which he described in his Traité de la Lumière (1690). His theory of light was initially rejected in favour of Newton's corpuscular theory of light, until Augustin-Jean Fresnel adapted Huygens's principle to give a complete explanation of the rectilinear propagation and diffraction effects of light in 1821. Today this principle is known as the Huygens–Fresnel principle. (Full article...)

Did you know (auto-generated) –

• ... that the music of math rock band Jyocho has been alternatively described as akin to "madness" or "contemplative and melancholy"?
• ... that mathematician Daniel Larsen was the youngest contributor to the New York Times crossword puzzle?
• ... that the discovery of Descartes' theorem in geometry came from a too-difficult mathematics problem posed to a princess?
• ... that Kit Nascimento, a spokesperson for the government of Guyana during the aftermath of Jonestown, disagrees with current proposals to open the former Jonestown site as a tourist attraction?
• ... that the identity of Cleo, who provided online answers to complex mathematics problems without showing any work, was revealed over a decade later in 2025?
• ... that despite a mathematical model deeming the ice cream bar flavour Goody Goody Gum Drops impossible, it was still created?
• ... that Green Day's "Wake Me Up When September Ends" became closely associated with the aftermath of Hurricane Katrina?
• ... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?

More did you know –

Did you know...

• ...that the sum of the first n odd numbers divided by the sum of the next n odd numbers is always equal to one third?
• ...that i to the power of i, where i is the square root of -1, is a real number?
• ...an infinite, nonrepeating decimal can be represented using only the number 1 using continued fractions?
• ...that 253931039382791 and the following 18 prime numbers all end in the digit 1?
• ...that the Electronic Frontier Foundation funds awards for the discovery of prime numbers beyond certain sizes?
• ...that pi can be computed using only the number 2 by the work of Viète?
• … that the Riemann Hypothesis, one of the Millennium Problems, depends on the asymptotic growth of the Mertens Function?

Selected article –

Image credit: User:Melchoir

The real number denoted by the recurring decimal 0.999… is exactly equal to 1. In other words, "0.999…" represents the same number as the symbol "1". Various proofs of this identity have been formulated with varying rigour, preferred development of the real numbers, background assumptions, historical context, and target audience.

The equality has long been taught in textbooks, and in the last few decades, researchers of mathematics education have studied the reception of this equation among students, who often reject the equality. The students' reasoning is typically based on one of a few common erroneous intuitions about the real numbers; for example, a belief that each unique decimal expansion must correspond to a unique number, an expectation that infinitesimal quantities should exist, that arithmetic may be broken, an inability to understand limits or simply the belief that 0.999… should have a last 9. These ideas are false with respect to the real numbers, which can be proven by explicitly constructing the reals from the rational numbers, and such constructions can also prove that 0.999… = 1 directly. (Full article...)

View all selected articles

Subcategories

Algebra | Arithmetic | Analysis | Complex analysis | Applied mathematics | Calculus | Category theory | Chaos theory | Combinatorics | Dynamical systems | Fractals | Game theory | Geometry | Algebraic geometry | Graph theory | Group theory | Linear algebra | Mathematical logic | Model theory | Multi-dimensional geometry | Number theory | Numerical analysis | Optimization | Order theory | Probability and statistics | Set theory | Statistics | Topology | Algebraic topology | Trigonometry | Linear programming

---

Mathematics | History of mathematics | Mathematicians | Awards | Education | Literature | Notation | Organizations | Theorems | Proofs | Unsolved problems

Full category tree. Select [►] to view subcategories.

Mathematics

Mathematics by country

Fields of mathematics

Mathematics-related lists

Mathematicians

Women in mathematics

Works about mathematics

Mathematics and art

Bruhat family

Choquet family

Mathematical classification systems

Mathematical concepts

Mathematical constants

Mathematics and culture

Eponyms in mathematics

Mathematical examples

FL-Class Polyhedra articles

History of mathematics

Mathematics occupations

Mathematical notation

Outlines of mathematics and logic

Philosophy of mathematics

Mathematical projects

Mathematical proofs

Pseudomathematics

Set index articles on mathematics

Mathematical terminology

Mathematical theorems

Mathematical tools

Mathematics stubs

Topics in mathematics

General	Foundations	Number theory	Discrete mathematics
Mathematicians History of mathematics Philosophy of mathematics Mathematical notation Mathematical beauty Mathematics education Glossary of mathematical symbols	Foundations of mathematics Mathematical logic Proof theory Gödel's incompleteness theorems Model theory Recursion theory Set theory Naive set theory Axiomatic set theory Category theory Topos theory	Number theory Algebraic number theory Analytic number theory Arithmetic Fundamental theorem of arithmetic Numbers Natural numbers Prime numbers Rational numbers Algebraic numbers	Discrete mathematics Combinatorics Combinatorial geometry Coding theory Combinatorial design Enumerative combinatorics Combinatorial optimization Graph theory Order theory Lattice theory Digital Signal Processing Theoretical computer science Computability theory Complexity theory
Algebra	Analysis	Geometry and topology	Applied mathematics
Algebra Elementary algebra Abstract algebra Group theory Ring theory Field theory Commutative algebra Geometric algebra Linear algebra Matrix theory Multilinear algebra Universal algebra Fundamental theorem of algebra	Analysis Calculus Fundamental theorem of calculus Vector calculus Geometric calculus Measure theory Real analysis Complex analysis Differential equations Ordinary differential equations Partial differential equations Integral equations Approximation theory Special functions Potential theory Harmonic analysis Fourier analysis Functional analysis Operator theory	Geometry Euclidean geometry Trigonometry Analytic geometry Non-Euclidean geometry Affine geometry Projective geometry Convex geometry Discrete geometry Algebraic geometry Differential geometry K theory Gauge theory Riemannian geometry Lie groups Topology General topology Algebraic topology Geometric topology Differential topology	Applied mathematics Mathematical modeling Mathematical physics Dynamical systems Control theory Calculus of variations Optimization Mathematical economics Game theory Mathematical finance Statistics Probability theory Stochastic processes Numerical analysis Cryptography Information theory

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Related portals

WikiProjects

The Mathematics WikiProject is the center for mathematics-related editing on Wikipedia. Join the discussion on the project's talk page.

Project pages

• Participants
• Current activity
• Manual of style
• Conventions

Essays

• Advice on using Wikipedia for mathematics self-study
• Proofs

Subprojects

• PlanetMath Exchange (Talk)
• Graphics (Talk)
• Article assessment (Talk)

Related projects

Computer science | Cryptography | Game theory | Numbers | Physics | Science | Statistics

Things you can do

• Create a new article: List of requested articles
• Add a new image: Image requests
• Expand an article: Mathematics stubs
• Lend your expertise: Expert attention needed

In other Wikimedia projects

The following Wikimedia Foundation sister projects provide more on this subject:

• 

  Commons
  Free media repository

• 

  Wikibooks
  Free textbooks and manuals

• 

  Wikidata
  Free knowledge base

• 

  Wikinews
  Free-content news

• 

  Wikiquote
  Collection of quotations

• 

  Wikisource
  Free-content library

• 

  Wikiversity
  Free learning tools

• 

  Wiktionary
  Dictionary and thesaurus

More portals

Discover Wikipedia using portals

• 

  List of all portals

• 

  The arts portal

• 

  Biography portal

• 

  Current events portal

• 

  Geography portal

• 

  History portal

• 

  Mathematics portal

• 

  Science portal

• 

  Society portal

• 

  Technology portal

• 

  Random portal

• 

  WikiProject Portals